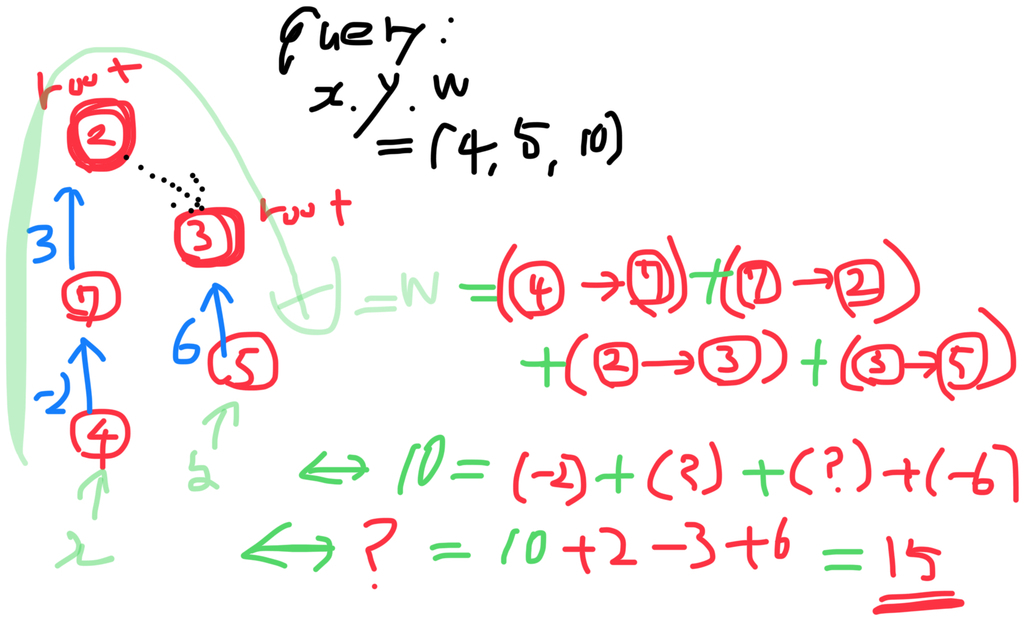これを解こうとしてできなかったのでまとめた。
judge.u-aizu.ac.jp
重み付きUnion-Find
英語名はよくわかんなくてweighted union-find とか weighted union heuristic、weighted disjoint set dataみたいに言われてるっぽい。Union-Find木に「あるノードから別のノードへのコスト」を加えたもの。Union-Find木自体の説明についてはAtcoderのTypical ContestかAOJのDSLに基本問題と解説があるのでチェケラ
atc001.contest.atcoder.jp
judge.u-aizu.ac.jp
ググった
ありがとうございます。
qiita.com
at274.hatenablog.com
喜び勇んで読んだが、いまいちなにをやっているのかわからんので整理する。
経路圧縮
- 木の葉を直接根にくっつけちまえ、という発想。これにより再帰的に遡ると最悪O(n)だったのがO(logn)となる（計算の理屈は知らん）。 - よくみかける「根を遡る処理の過程で親を根に直接つなぎかえる」メソッドだと、そのメソッドが呼ばれたあとに併合すると高さが増える。よくみかける実装だとその次のクエリでメソッドを呼ぶ際につなぎかえる
ランク付け
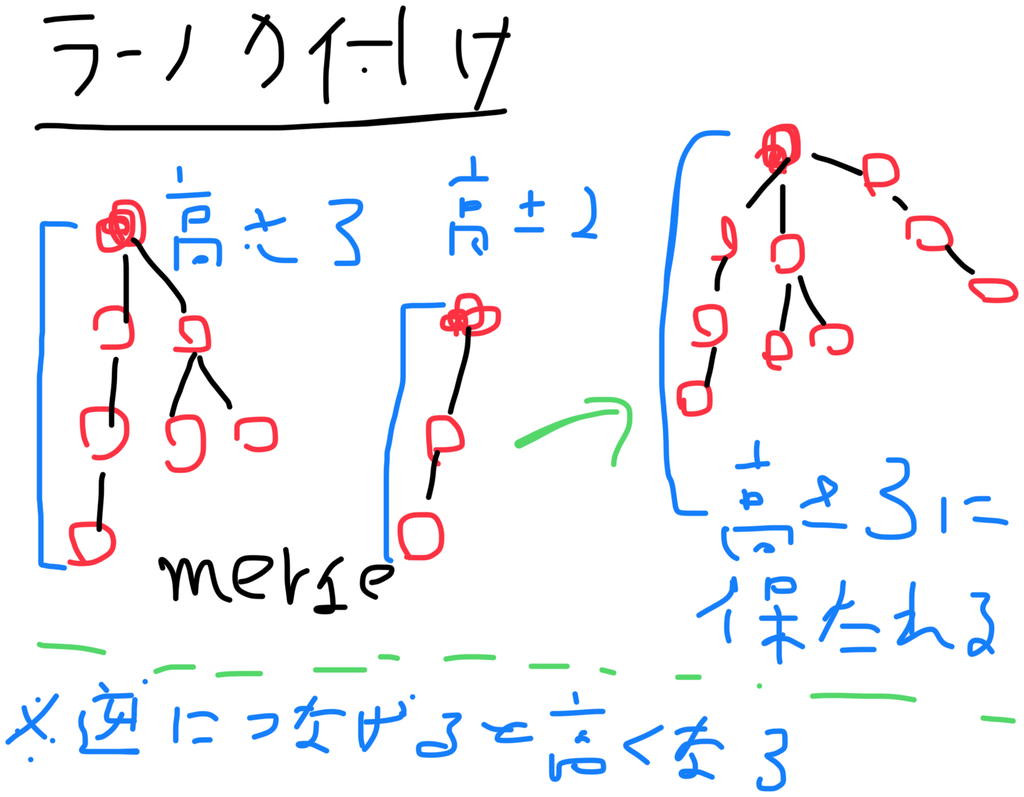
- 根に木の高さの情報をもたせておく。「各ノード」じゃなくて根のノードだけにもたせるのは木の根同士だけを比較すれば充分だから、と思っている。実装が楽だし
- 併合の際に低いほうの根の親を木の高いほうの根にすることで、計算の前後で木の高さを保つことができる
- 木の高さが低いとその分再帰が浅くなるので計算が早くなる
- これもO(logn)らしいが計算方法など知る由もない
この二つはUnion-Findの高速化としていろいろな場所で書かれているが、なぜか重み付きUnon-Findはこれらのテクニックを二つとも使った実装しか見当たらない。どうせ「Union-Findくらいみんなライブラリにもってて当然のように圧縮もランク付けも実装してるんだろうし、それらを流用するのが前提で説明してやんよ」ということなのだろう。余計なお世話だ。
重み
さきほどggった資料のうちqiitaのほうにこのような記述がある。
最初の
w += weight(x); w -= weight(y);
と補正するところが少しわかりにくいかもしれません。merge(x, y) 操作では、元々の x と y との間に辺を繋ぐのではなく、root(x) と root(y) の間をつなぐので、つなぐべき辺の重みは w ではなく修正が必要になります。
これを105回くらい読んでも式の意味がわからなかったので書いた。
まず、各ノードにもたせるコスト（重さ）とはなんなのか。これはノードと、そのノードと直上の親とのコストの差分である。
併合のクエリx y wとは、ノードxからノードyへのコストがwということである。 
したがって上図で5から4までのコストは、通るパスの重さをすべて足し合わせたもので、6+3 = 9ということになる。
xからyへのコストがwということは、逆を言えばyからxへのコストが-wということなので、 
したがって、たとえばx=8, y=5のコストを求めると、
8から4のノードのコスト + 4から2のノードのコスト + 2から5のノードのコスト
= (-3) + (-3) + (-6)
= -12
になる。
よくある実装ではこれを併合のときに計算していて、異なる木に属する2つのノードどうしを結ぶとき、
w = (xからxの根までのコスト) + (xの根からyの根までのコスト) + (yの根からyまでのコスト)
とやっている。図で示すとこんな感じ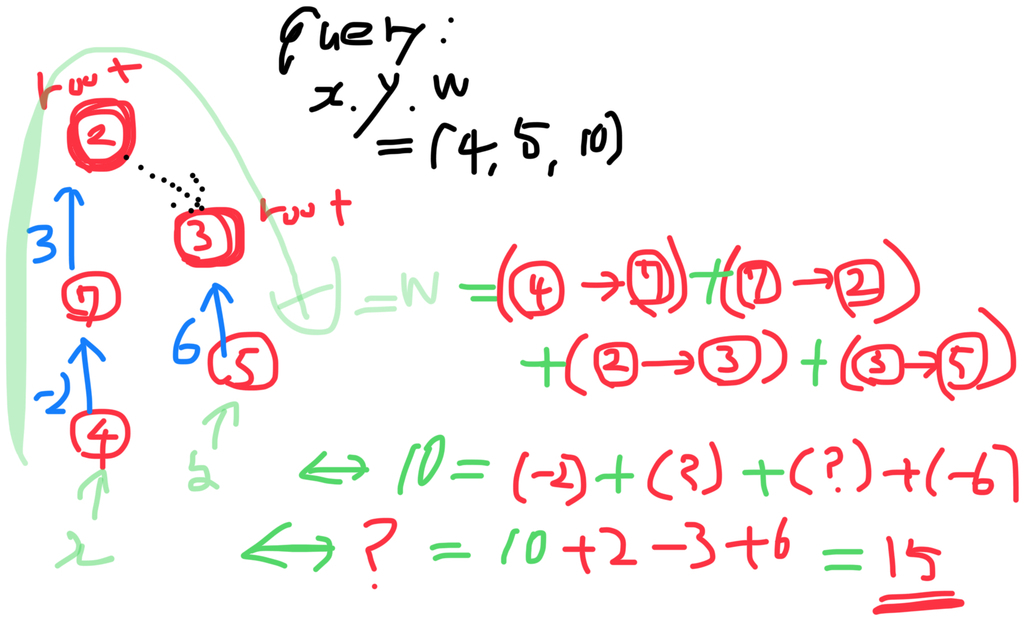 
求めるのは新しくエッジを貼った「xの根からyの根までのコスト」なので、先程の式は
(xの根からyの根までのコスト) = w - (xからxの根までのコスト + yの根からyまでのコスト)
であり、
yの根からyへのコスト = - (yからyの根へのコスト)
なので、結局
(xの根からyの根までのコスト) = w - (xからxの根までのコスト - yからyの根までのコスト)
というわけ。ランク付けを使うと高さの低い木の根から高い木の根にエッジを貼るので、
木xのほうが低い場合：
x -> xの根 -> xの根からyの根 -> yの根からy
木yのほうが低い場合：
y -> yの根 -> yの根からxの根 -> xの根からx
となり、後者の累積和は単純に前者の符号を反転したものになる。なのでランクの大小の比較でそれを判定しているわけ。
これで骨子は分かったと思うので適当に実装していけばいいです。
高速化なしの実装
提出先はAOJのDSL。通らないのは知っててやる。世のサンプルコードすべてが正しくAC通るものと思うなよ（自戒）。「私はわざとジャッジサーバを無駄に回しました」という札を首から下げながら提出。
import sys
sys.setrecursionlimit(10**9)
class WeightedUnionFindTree:
def __init__(self, n):
self.par = list(range(n))
self.weight = [0 for _ in range(n)]
def root(self, t):
if t == self.par[t]:
return t
return self.root(self.par[t])
def rec_weight(self, t):
if t == self.par[t]:
return 0
return self.weight[t] + self.rec_weight(self.par[t])
def same(self, x, y):
return self.root(x) == self.root(y)
def unite(self, x, y, w):
rootx = self.root(x)
rooty = self.root(y)
if rootx != rooty:
self.weight[rootx] += w - self.rec_weight(x)
self.par[rootx] = y
def diff(self, x, y):
if self.same(x, y):
return self.rec_weight(x) - self.rec_weight(y)
else:
return "?"
n, q = list(map(int, input().split()))
wuft = WeightedUnionFindTree(n)
for _ in range(q):
query = list(map(int, input().split()))
if query[0] == 0:
x, y, w = query[1], query[2], query[3]
wuft.unite(x, y, w)
elif query[0] == 1:
x, y = query[1], query[2]
print(wuft.diff(x, y))
でこれが当然のようにTLEとなる。ので、高速化テクニックのいずれかを実装する。世のサンプルが両方とも使っているのしか見つからなかったことはさきほど述べたが、天の邪鬼なのとちゃんと動くのかのテストもかねて、経路圧縮だけを実装する。
重みつきUnion-Find（path compression）
root()と、併合処理の場合分けをしただけ。
import sys
sys.setrecursionlimit(10**9)
"""
重み付きで経路圧縮
ランクでの比較は考えず、圧縮だけする
"""
class WeightedUnionFindTree:
def __init__(self, n):
self.par = list(range(n))
self.weight = [0 for _ in range(n)]
def root(self, t):
if t == self.par[t]:
return t
r = self.root(self.par[t])
self.weight[t] += self.weight[self.par[t]]
self.par[t] = r
return r
def rec_weight(self, t):
if t == self.par[t]:
return 0
return self.weight[t] + self.rec_weight(self.par[t])
def same(self, x, y):
return self.root(x) == self.root(y)
def unite(self, x, y, w):
rootx = self.root(x)
rooty = self.root(y)
if rootx != rooty:
if y != rooty:
self.weight[rootx] = w - self.rec_weight(x)
else:
self.weight[rootx] = w - (self.weight[x] - self.weight[y])
self.par[rootx] = y
def diff(self, x, y):
if self.same(x, y):
return self.rec_weight(x) - self.rec_weight(y)
else:
return "?"
n, q = list(map(int, input().split()))
wuft = WeightedUnionFindTree(n)
for _ in range(q):
query = list(map(int, input().split()))
if query[0] == 0:
x, y, w = query[1], query[2], query[3]
wuft.unite(x, y, w)
elif query[0] == 1:
x, y = query[1], query[2]
print(wuft.diff(x, y))
併合するときにyが葉かどうかで処理を分けているのは、葉だと
w = xからxの根までのコスト + xの根からyの根までのコスト
xの根からyの根までのコスト = w - xからxの根までのコスト
でyの木のコストを考えずにつなげればいいだけなので。葉以外だと↑で既にあげている感じでいい。
例題 ABC087 D - People on a Line
ということでqiitaのほうの参考でも挙げられていたこれをやる。めんどくさいのでクラスで管理はせず、配列だけでやった。
n, m = list(map(int, input().split()))
par = list(range(n+1))
dis = [0] * (n+1)
def root(x):
if x == par[x]:
return x
r = root(par[x])
dis[x] += dis[par[x]]
par[x] = r
return r
def cost(x):
if x == par[x]:
return 0
return dis[x] + cost(par[x])
for _ in range(m):
l, r, d = list(map(int, input().split()))
rootl, rootr = root(l), root(r)
if rootl != rootr:
if r != rootr:
dis[rootl] = d - cost(l)
else:
dis[rootl] = d - (cost(l) - cost(r))
par[rootl] = r
else:
if d != cost(l) - cost(r):
print("No")
exit()
print("Yes")
はい。よくできました。
----- 追記 2020-06-24 -----
AOJ DSL 1_Bをgolangで解いたが、参考にこの記事を見返したら自分で書いたというのに分かりにくくて絶望した。解読したらちょっと簡略化できた。costを再帰的に回すのもめんどくさいので、weight[i]をiの直接の親へのコストではなく、iから根へのコストとしてみた。（はてなブログのバグか？なんかしらんけどmarkdown再編集できないんだが...）
package main
import "fmt"
func main(){
var N, Q int
fmt.Scan(&N, &Q)
parent := make([]int, N)
weight := make([]int, N)
for i:=0; i<N; i++{
parent[i] = i
}
var root func(i int)int
var union func(i, j, k int)
root = func(x int)int{
if x == parent[x]{
return x
}
y := root(parent[x])
weight[x] += weight[parent[x]]
parent[x] = y
return y
}
union = func(a, b, w int){
ra, rb := root(a), root(b)
if ra != rb{
if b == rb{
// w = aからaの根+aの根からbの根
weight[ra] = w - weight[a]
}else{
// w = aからaの根+aの根からbの根+bの根からb
// w = aからaの根+aの根からbの根-bからbの根
weight[ra] = w - (weight[a]-weight[b])
}
parent[ra] = rb // これポイント
}
}
for i:=0; i<Q; i++{
var query int
fmt.Scan(&query)
if query == 0{
var x, y, z int
fmt.Scan(&x, &y, &z)
union(x, y, z)
}else{
var x, y int
fmt.Scan(&x, &y)
if root(x) != root(y){
fmt.Println("?")
}else{
fmt.Println(weight[x]-weight[y])
}
}
}
}
verify
